17.2. 价值迭代¶ 在 SageMaker Studio Lab 中打开 Notebook
在本节中,我们将讨论如何在每个状态下为机器人选择最佳动作,以最大限度地提高轨迹的“回报”。我们将描述一种名为价值迭代的算法,并为一个在冰湖上移动的模拟机器人实现它。
17.2.1. 随机策略¶
表示为 \(\pi(a \mid s)\) 的随机策略(简称策略)是给定状态 \(s \in \mathcal{S}\) 下动作 \(a \in \mathcal{A}\) 的条件分布,即 \(\pi(a \mid s) \equiv P(a \mid s)\)。举个例子,如果机器人有四个动作 \(\mathcal{A}=\) {向左、向下、向右、向上}。在状态 \(s \in \mathcal{S}\) 下,针对这组动作 \(\mathcal{A}\) 的策略是一个分类分布,其中四个动作的概率可能是 \([0.4, 0.2, 0.1, 0.3]\);在其他某个状态 \(s' \in \mathcal{S}\),这四个相同动作的概率 \(\pi(a \mid s')\) 可能是 \([0.1, 0.1, 0.2, 0.6]\)。请注意,对于任何状态 \(s\),我们都应该有 \(\sum_a \pi(a \mid s) = 1\)。确定性策略是随机策略的一种特殊情况,即分布 \(\pi(a \mid s)\) 只对一个特定动作给出非零概率,例如,在我们有四个动作的例子中,概率为 \([1, 0, 0, 0]\)。
为了使符号不那么繁琐,我们通常将条件分布写为 \(\pi(s)\),而不是 \(\pi(a \mid s)\)。
17.2.2. 价值函数¶
现在想象一下,机器人从一个状态 \(s_0\) 开始,在每个时刻,它首先从策略 \(a_t \sim \pi(s_t)\) 中采样一个动作,并执行这个动作以达到下一个状态 \(s_{t+1}\)。轨迹 \(\tau = (s_0, a_0, r_0, s_1, a_1, r_1, \ldots)\) 可能会有所不同,这取决于在中间时刻采样到的具体动作 \(a_t\)。我们定义所有这些轨迹的平均“回报” \(R(\tau) = \sum_{t=0}^\infty \gamma^t r(s_t, a_t)\)
其中 \(s_{t+1} \sim P(s_{t+1} \mid s_t, a_t)\) 是机器人的下一个状态,而 \(r(s_t, a_t)\) 是在时间 \(t\) 于状态 \(s_t\) 执行动作 \(a_t\) 所获得的瞬时奖励。这被称为策略 \(\pi\) 的“价值函数”。简单来说,状态 \(s_0\) 对于策略 \(\pi\) 的价值,表示为 \(V^\pi(s_0)\),是机器人如果从状态 \(s_0\) 开始并在每个时刻根据策略 \(\pi\) 采取行动所获得的期望 \(\gamma\)-折扣“回报”。
接下来,我们将轨迹分解为两个阶段:(i) 第一阶段,对应于执行动作 \(a_0\) 后从 \(s_0 \to s_1\) 的过程,以及 (ii) 第二阶段,即其后的轨迹 \(\tau' = (s_1, a_1, r_1, \ldots)\)。强化学习中所有算法背后的关键思想是,状态 \(s_0\) 的价值可以写成第一阶段获得的平均奖励与在所有可能的下一状态 \(s_1\) 上的价值函数的平均值之和。这非常直观,并且源于我们的马尔可夫假设:从当前状态出发的平均回报是去往下一状态的平均奖励与从下一状态出发的平均回报之和。在数学上,我们将这两个阶段写为
这种分解非常强大:它是动态规划原理的基础,所有强化学习算法都基于此原理。注意,第二阶段有两个期望,一个是对第一阶段使用随机策略选择的动作 \(a_0\) 的期望,另一个是对从所选动作中获得的可能状态 \(s_1\) 的期望。我们可以使用马尔可夫决策过程 (MDP) 中的转移概率将 (17.2.2) 写成
这里需要注意的一个重要点是,上述恒等式对所有状态 \(s \in \mathcal{S}\) 都成立,因为我们可以想象任何从该状态开始的轨迹,并将其分解为两个阶段。
17.2.3. 动作-价值函数¶
在实现中,维护一个称为“动作价值”函数的量通常很有用,它与价值函数密切相关。这被定义为从 \(s_0\) 开始,但第一阶段的动作固定为 \(a_0\) 的轨迹的平均“回报”
注意,期望内的求和是从 \(t=1,\ldots, \infty\) 开始的,因为在这种情况下第一阶段的奖励是固定的。我们可以再次将轨迹分解为两部分并写成
这个版本是 (17.2.3) 在动作价值函数上的模拟。
17.2.4. 最优随机策略¶
价值函数和动作价值函数都取决于机器人选择的策略。接下来我们将考虑能够实现最大平均“回报”的“最优策略”
在机器人可能采取的所有随机策略中,最优策略 \(\pi^*\) 为从状态 \(s_0\) 开始的轨迹实现了最大的平均折扣“回报”。让我们将最优策略的价值函数和动作价值函数表示为 \(V^* \equiv V^{\pi^*}\) 和 \(Q^* \equiv Q^{\pi^*}\)。
让我们观察一个确定性策略,在该策略下,在任何给定状态下只有一个可能的动作。这给了我们
一个很好的记忆方法是:状态 \(s\) 下的最优动作(对于确定性策略)是最大化第一阶段的奖励 \(r(s, a)\) 和从下一状态 \(s'\) 开始的轨迹的平均“回报”之和的那个动作,该平均“回报”是在第二阶段所有可能的下一状态 \(s'\) 上取平均得到的。
17.2.5. 动态规划原理¶
我们在上一节中关于 (17.2.2) 或 (17.2.5) 的推导可以转化为一种算法,用于分别计算最优价值函数 \(V^*\) 或动作价值函数 \(Q^*\)。观察到
对于一个确定性的最优策略 \(\pi^*\),由于在状态 \(s\) 下只有一个动作可以执行,我们也可以写成
对于所有状态 \(s \in \mathcal{S}\)。这个恒等式被称为“动态规划原理” (Bellman, 1952, Bellman, 1957)。它由理查德·贝尔曼在1950年代提出,我们可以将其记为“最优轨迹的剩余部分也是最优的”。
17.2.6. 价值迭代¶
我们可以将动态规划原理转化为一种寻找最优价值函数的算法,称为价值迭代。价值迭代的关键思想是将这个恒等式看作一组将不同状态 \(s \in \mathcal{S}\) 下的 \(V^*(s)\) 联系起来的约束。我们为所有状态 \(s \in \mathcal{S}\) 将价值函数 \(V_0(s)\) 初始化为任意值。在第 \(k^{\textrm{th}}\) 次迭代中,价值迭代算法按如下方式更新价值函数:
事实证明,当 \(k \to \infty\) 时,无论初始值 \(V_0\) 如何,价值迭代算法估计的价值函数都会收敛到最优价值函数,
同样的价值迭代算法也可以等价地使用动作-价值函数写成:
在这种情况下,我们为所有 \(s \in \mathcal{S}\) 和 \(a \in \mathcal{A}\) 将 \(Q_0(s, a)\) 初始化为一些任意值。同样,我们有 \(Q^*(s, a) = \lim_{k \to \infty} Q_k(s, a)\) 对所有 \(s \in \mathcal{S}\) 和 \(a \in \mathcal{A}\) 成立。
17.2.7. 策略评估¶
价值迭代使我们能够计算最优确定性策略 \(\pi^*\) 的最优价值函数,即 \(V^{\pi^*}\)。我们也可以使用类似的迭代更新来计算与任何其他潜在随机策略 \(\pi\) 相关联的价值函数。我们再次为所有状态 \(s \in \mathcal{S}\) 将 \(V^\pi_0(s)\) 初始化为一些任意值,并在第 \(k^{\textrm{th}}\) 次迭代中执行更新
该算法被称为策略评估,可用于在给定策略的情况下计算价值函数。同样,事实证明,当 \(k \to \infty\) 时,这些更新会收敛到正确的价值函数,而不管初始值 \(V_0\) 如何,
计算策略 \(\pi\) 的动作价值函数 \(Q^\pi(s, a)\) 的算法是类似的。
17.2.8. 价值迭代的实现¶
接下来我们展示如何为一个名为“冰湖”(FrozenLake)的导航问题实现价值迭代,该问题来自 OpenAI Gym。我们首先需要按以下代码所示设置环境。
%matplotlib inline
import random
import numpy as np
from d2l import torch as d2l
seed = 0 # Random number generator seed
gamma = 0.95 # Discount factor
num_iters = 10 # Number of iterations
random.seed(seed) # Set the random seed to ensure results can be reproduced
np.random.seed(seed)
# Now set up the environment
env_info = d2l.make_env('FrozenLake-v1', seed=seed)
在冰湖环境中,机器人移动在一个 \(4 \times 4\) 的网格上(这些是状态),动作包括“上”(\(\uparrow\))、“下”(\(\rightarrow\))、“左”(\(\leftarrow\))和“右”(\(\rightarrow\))。环境中包含一些洞(H)单元格和冰面(F)单元格,以及一个目标(G)单元格,所有这些对机器人来说都是未知的。为了简化问题,我们假设机器人的动作是可靠的,即对于所有 \(s \in \mathcal{S}, a \in \mathcal{A}\),\(P(s' \mid s, a) = 1\)。如果机器人到达目标,则试验结束,机器人获得奖励 \(1\),无论采取何种动作;在任何其他状态下,所有动作的奖励均为 \(0\)。机器人的目标是学习一个策略,使其能够从给定的起始位置(S)(即 \(s_0\))到达目标位置(G),以最大化“回报”。
以下函数实现了价值迭代,其中 env_info 包含MDP和环境相关信息,gamma 是折扣因子
def value_iteration(env_info, gamma, num_iters):
env_desc = env_info['desc'] # 2D array shows what each item means
prob_idx = env_info['trans_prob_idx']
nextstate_idx = env_info['nextstate_idx']
reward_idx = env_info['reward_idx']
num_states = env_info['num_states']
num_actions = env_info['num_actions']
mdp = env_info['mdp']
V = np.zeros((num_iters + 1, num_states))
Q = np.zeros((num_iters + 1, num_states, num_actions))
pi = np.zeros((num_iters + 1, num_states))
for k in range(1, num_iters + 1):
for s in range(num_states):
for a in range(num_actions):
# Calculate \sum_{s'} p(s'\mid s,a) [r + \gamma v_k(s')]
for pxrds in mdp[(s,a)]:
# mdp(s,a): [(p1,next1,r1,d1),(p2,next2,r2,d2),..]
pr = pxrds[prob_idx] # p(s'\mid s,a)
nextstate = pxrds[nextstate_idx] # Next state
reward = pxrds[reward_idx] # Reward
Q[k,s,a] += pr * (reward + gamma * V[k - 1, nextstate])
# Record max value and max action
V[k,s] = np.max(Q[k,s,:])
pi[k,s] = np.argmax(Q[k,s,:])
d2l.show_value_function_progress(env_desc, V[:-1], pi[:-1])
value_iteration(env_info=env_info, gamma=gamma, num_iters=num_iters)
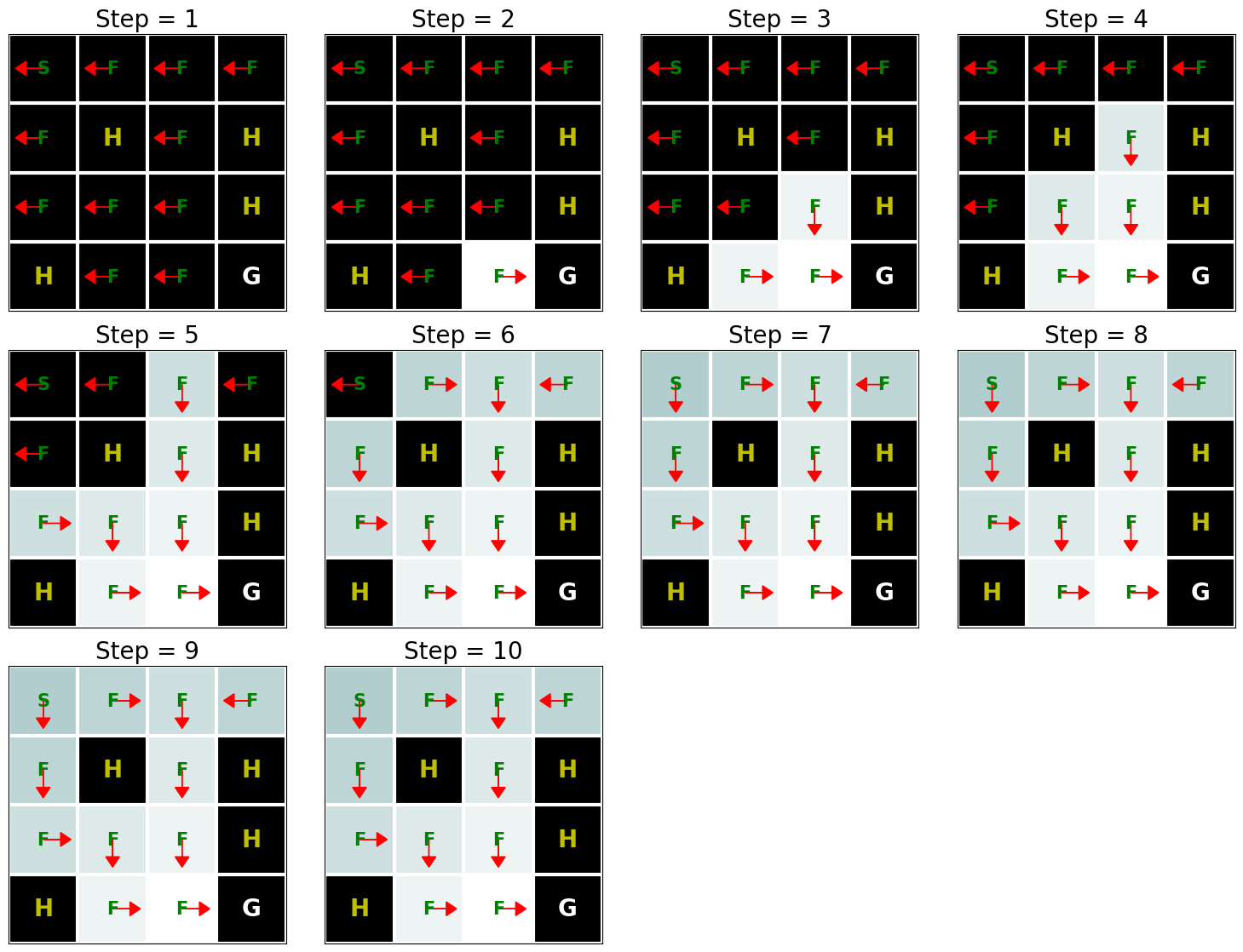
上图显示了策略(箭头指示动作)和价值函数(颜色变化显示了价值函数如何从初始值(深色)随时间变化到最优值(浅色))。如我们所见,价值迭代在10次迭代后找到了最优价值函数,并且只要不是H单元格,从任何状态开始都可以到达目标状态(G)。该实现的另一个有趣之处在于,除了找到最优价值函数,我们还自动找到了与此价值函数对应的最优策略 \(\pi^*\)。
17.2.9. 总结¶
价值迭代算法背后的主要思想是利用动态规划原理来找到从给定状态获得的最优平均回报。请注意,实现价值迭代算法需要我们完全了解马尔可夫决策过程(MDP),例如转移函数和奖励函数。
