17.3. Q-Learning¶ 在 SageMaker Studio Lab 中打开 Notebook
在上一节中,我们讨论了值迭代算法,它需要访问完整的马尔可夫决策过程(MDP),例如转移函数和奖励函数。在本节中,我们将探讨Q学习 (Watkins and Dayan, 1992),这是一种无需了解MDP即可学习价值函数的算法。该算法体现了强化学习的核心思想:它将使机器人能够获取自己的数据。
17.3.1. Q学习算法¶
回想一下,在值迭代中,动作-价值函数的值迭代对应于以下更新
正如我们所讨论的,实现这个算法需要知道MDP,特别是转移函数 \(P(s' \mid s, a)\)。Q学习的关键思想是用机器人访问过的状态上的求和来代替上述表达式中对所有 \(s' \in \mathcal{S}\) 的求和。这使我们能够避免知道转移函数的需要。
17.3.2. Q学习背后的优化问题¶
让我们想象一下,机器人使用一个策略 \(\pi_e(a \mid s)\) 来采取行动。就像上一章一样,它收集一个数据集,包含 \(n\) 条轨迹,每条轨迹有 \(T\) 个时间步 \(\{ (s_t^i, a_t^i)_{t=0,\ldots,T-1}\}_{i=1,\ldots, n}\)。回想一下,值迭代实际上是一组约束,将不同状态和动作的动作-价值 \(Q^*(s, a)\) 相互联系起来。我们可以使用机器人通过 \(\pi_e\) 收集的数据来实现一个近似版本的值迭代:
我们首先观察一下这个表达式与上面的值迭代之间的异同。如果机器人的策略 \(\pi_e\) 等于最优策略 \(\pi^*\),并且它收集了无限量的数据,那么这个优化问题将与值迭代背后的优化问题相同。但是,值迭代需要我们知道 \(P(s' \mid s, a)\),而这个优化目标没有这一项。我们并没有作弊:当机器人使用策略 \(\pi_e\) 在状态 \(s_t^i\) 采取动作 \(a_t^i\) 时,下一个状态 \(s_{t+1}^i\) 是从转移函数中抽样的样本。所以优化目标也间接地通过机器人收集的数据获得了转移函数的信息。
我们优化问题的变量是所有 \(s \in \mathcal{S}\) 和 \(a \in \mathcal{A}\) 的 \(Q(s, a)\)。我们可以使用梯度下降来最小化目标函数。对于我们数据集中的每一对 \((s_t^i, a_t^i)\),我们可以写出:
其中 \(\alpha\) 是学习率。通常在实际问题中,当机器人到达目标位置时,轨迹结束。这种终止状态的价值为零,因为机器人在此状态之后不再采取任何行动。我们应该修改我们的更新来处理这类状态:
其中 \(\mathbb{1}_{s_{t+1}^i \textrm{ is terminal}}\) 是一个指示变量,如果 \(s_{t+1}^i\) 是一个终止状态,则为1,否则为0。不在数据集中的状态-动作对 \((s, a)\) 的值被设为 \(-\infty\)。这个算法被称为Q学习。
给定这些更新的解 \(\hat{Q}\),它是最优价值函数 \(Q^*\) 的一个近似,我们可以很容易地得到与该价值函数对应的最优确定性策略:
在某些情况下,可能存在多个确定性策略对应于同一个最优价值函数;因为它们的价值函数相同,所以可以任意打破这种平局。
17.3.3. Q学习中的探索¶
机器人用于收集数据的策略 \(\pi_e\) 对确保Q学习良好工作至关重要。毕竟,我们已经用机器人收集的数据代替了使用转移函数 \(P(s' \mid s, a)\) 对 \(s'\) 的期望。如果策略 \(\pi_e\) 没有达到状态-动作空间的不同部分,那么很容易想象我们的估计 \(\hat{Q}\) 将会是 \(Q^*\) 的一个很差的近似。同样重要的是要注意,在这种情况下,对*所有状态* \(s \in \mathcal{S}\) 的 \(Q^*\) 的估计都会很差,而不仅仅是 \(\pi_e\) 访问过的那些状态。这是因为Q学习目标(或值迭代)是一个将所有状态-动作对的价值联系在一起的约束。因此,选择正确的策略 \(\pi_e\) 来收集数据至关重要。
我们可以通过选择一个完全随机的策略 \(\pi_e\) 来缓解这个问题,该策略从 \(\mathcal{A}\) 中均匀随机地采样动作。这样的策略会访问所有状态,但需要大量的轨迹才能做到这一点。
因此,我们得出了Q学习的第二个关键思想,即探索。Q学习的典型实现将当前对 \(Q\) 的估计与策略 \(\pi_e\) 联系起来,设置为:
其中 \(\epsilon\) 被称为“探索参数”,由用户选择。策略 \(\pi_e\) 被称为探索策略。这种特定的 \(\pi_e\) 被称为 \(\epsilon\)-贪心探索策略,因为它以 \(1-\epsilon\) 的概率选择最优动作(在当前估计 \(\hat{Q}\) 下),但以剩余的 \(\epsilon\) 概率进行随机探索。我们也可以使用所谓的softmax探索策略:
其中超参数 \(T\) 被称为温度。在 \(\epsilon\)-贪心策略中较大的 \(\epsilon\) 值与softmax策略中较大的温度 \(T\) 值功能相似。
值得注意的是,当我们选择一个依赖于动作-价值函数 \(\hat{Q}\) 当前估计的探索策略时,我们需要周期性地解决优化问题。Q学习的典型实现是在使用 \(\pi_e\) 采取每个动作后,使用收集到的数据集中的几个状态-动作对(通常是机器人上一个时间步收集到的)进行一次小批量更新。
17.3.4. Q学习的“自我纠正”特性¶
在Q学习过程中,机器人收集的数据集随时间增长。探索策略 \(\pi_e\) 和估计 \(\hat{Q}\) 都随着机器人收集更多数据而演变。这为我们提供了关于Q学习为何有效的关键见解。考虑一个状态 \(s\):如果某个动作 \(a\) 在当前估计 \(\hat{Q}(s,a)\) 下具有较大的值,那么 \(\epsilon\)-贪心和softmax探索策略都会有更大的概率选择这个动作。如果这个动作实际上并*不是*理想的动作,那么由这个动作产生的未来状态将会有较差的奖励。因此,Q学习目标的下一次更新将减少值 \(\hat{Q}(s,a)\),这将降低机器人下次访问状态 \(s\) 时选择该动作的概率。坏的动作,例如那些在 \(\hat{Q}(s,a)\) 中被高估的动作,会被机器人探索到,但它们的值会在Q学习目标的下一次更新中被纠正。好的动作,例如那些值 \(\hat{Q}(s, a)\) 很大的动作,会被机器人更频繁地探索,从而得到加强。这个特性可以用来证明,即使Q学习从一个随机策略 \(\pi_e\) 开始,它也可以收敛到最优策略 (Watkins and Dayan, 1992)。
这种不仅能收集新数据,还能收集到正确类型数据的能力,是强化学习算法的核心特征,也是它们与监督学习的区别所在。使用深度神经网络的Q学习(我们稍后将在DQN章节中看到),是强化学习复兴的原因 (Mnih et al., 2013)。
17.3.5. Q学习的实现¶
我们现在展示如何在 Open AI Gym 的 FrozenLake 环境中实现Q学习。注意,这与我们在 值迭代 实验中考虑的设置相同。
%matplotlib inline
import random
import numpy as np
from d2l import torch as d2l
seed = 0 # Random number generator seed
gamma = 0.95 # Discount factor
num_iters = 256 # Number of iterations
alpha = 0.9 # Learing rate
epsilon = 0.9 # Epsilon in epsilion gready algorithm
random.seed(seed) # Set the random seed
np.random.seed(seed)
# Now set up the environment
env_info = d2l.make_env('FrozenLake-v1', seed=seed)
在FrozenLake环境中,机器人在一个 \(4 \times 4\) 的网格(这些是状态)上移动,动作有“上”(\(\uparrow\))、“下”(\(\rightarrow\))、“左”(\(\leftarrow\))和“右”(\(\rightarrow\))。环境中包含一些洞(H)单元格和冰冻(F)单元格,以及一个目标(G)单元格,所有这些对机器人来说都是未知的。为了简化问题,我们假设机器人的动作是可靠的,即对于所有 \(s \in \mathcal{S}, a \in \mathcal{A}\),\(P(s' \mid s, a) = 1\)。如果机器人到达目标,试验结束,机器人获得奖励 \(1\),无论采取何种动作;在任何其他状态下,所有动作的奖励都是 \(0\)。机器人的目标是学习一个策略,从给定的起始位置(S)(这是 \(s_0\))到达目标位置(G),以最大化*回报*。
我们首先实现 \(\epsilon\)-贪心方法如下:
def e_greedy(env, Q, s, epsilon):
if random.random() < epsilon:
return env.action_space.sample()
else:
return np.argmax(Q[s,:])
我们现在准备实现Q学习
def q_learning(env_info, gamma, num_iters, alpha, epsilon):
env_desc = env_info['desc'] # 2D array specifying what each grid item means
env = env_info['env'] # 2D array specifying what each grid item means
num_states = env_info['num_states']
num_actions = env_info['num_actions']
Q = np.zeros((num_states, num_actions))
V = np.zeros((num_iters + 1, num_states))
pi = np.zeros((num_iters + 1, num_states))
for k in range(1, num_iters + 1):
# Reset environment
state, done = env.reset(), False
while not done:
# Select an action for a given state and acts in env based on selected action
action = e_greedy(env, Q, state, epsilon)
next_state, reward, done, _ = env.step(action)
# Q-update:
y = reward + gamma * np.max(Q[next_state,:])
Q[state, action] = Q[state, action] + alpha * (y - Q[state, action])
# Move to the next state
state = next_state
# Record max value and max action for visualization purpose only
for s in range(num_states):
V[k,s] = np.max(Q[s,:])
pi[k,s] = np.argmax(Q[s,:])
d2l.show_Q_function_progress(env_desc, V[:-1], pi[:-1])
q_learning(env_info=env_info, gamma=gamma, num_iters=num_iters, alpha=alpha, epsilon=epsilon)
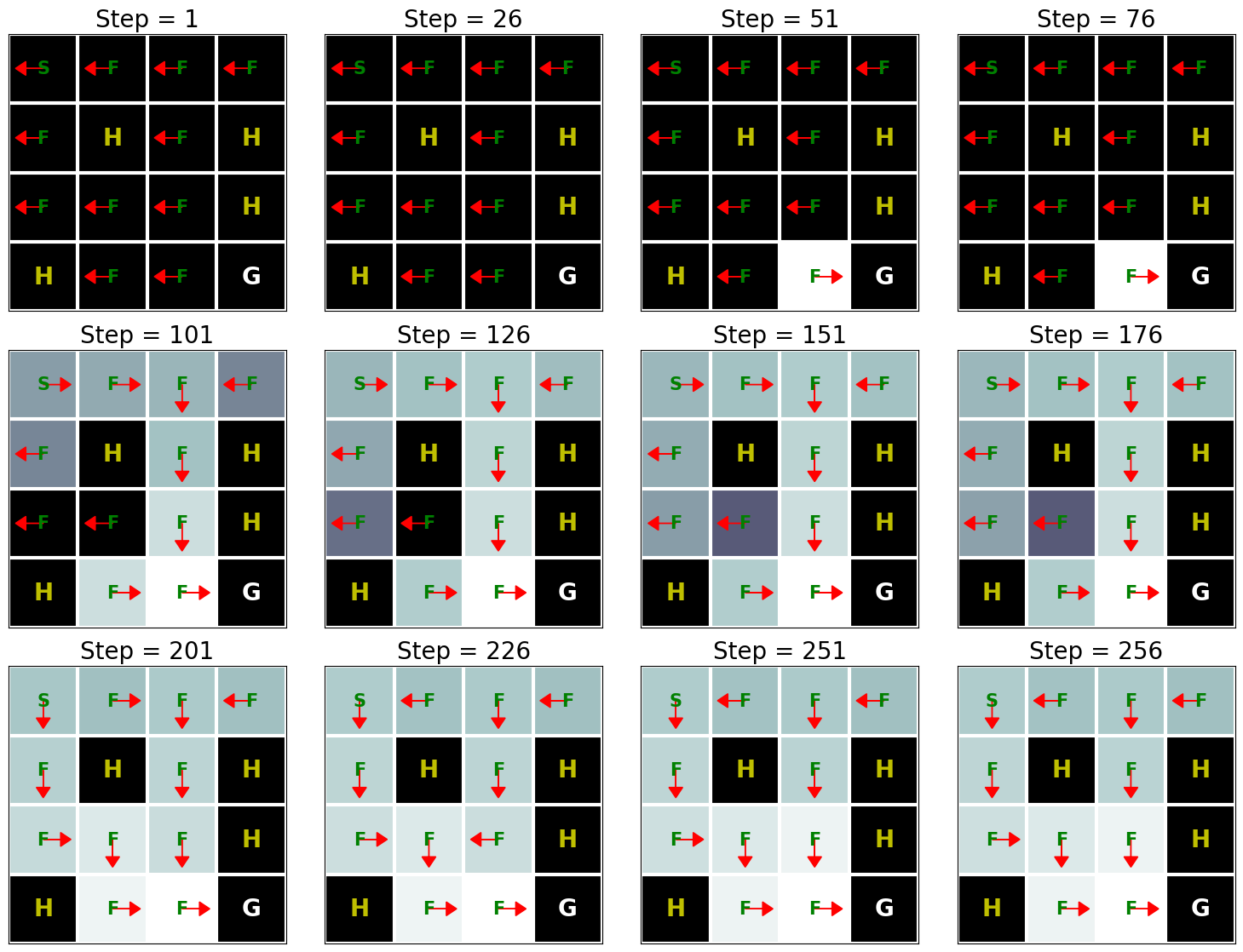
这个结果表明,Q学习大约在250次迭代后可以找到这个问题的最优解。然而,当我们将这个结果与值迭代算法的结果(参见值迭代的实现)进行比较时,我们可以看到值迭代算法需要少得多的迭代次数来找到这个问题的最优解。这是因为值迭代算法可以访问完整的MDP,而Q学习则不能。
17.3.6. 小结¶
Q学习是最基本的强化学习算法之一。它一直处于近期强化学习成功的中心,尤其是在学习玩视频游戏方面 (Mnih et al., 2013)。实现Q学习不需要我们完全了解马尔可夫决策过程(MDP),例如转移函数和奖励函数。
