9.1. 序列

Colab [pytorch]

在 Colab 中打开 Notebook

Colab [mxnet]

在 Colab 中打开 Notebook

Colab [jax]

在 Colab 中打开 Notebook

Colab [tensorflow]

在 Colab 中打开 Notebook

SageMaker Studio Lab

在 SageMaker Studio Lab 中打开 Notebook

到目前为止，我们专注于模型输入为单个特征向量 \(\mathbf{x} \in \mathbb{R}^d\) 的情况。当我们开发能够处理序列的模型时，主要的视角转变是我们现在关注由一系列有序特征向量 \(\mathbf{x}_1, \dots, \mathbf{x}_T\) 组成的输入，其中每个特征向量 \(\mathbf{x}_t\) 由时间步 \(t \in \mathbb{Z}^+\) 索引，并位于 \(\mathbb{R}^d\) 中。

有些数据集由单个巨大的序列组成。例如，气候科学家可能获得的极长传感器读数流。在这种情况下，我们可以通过随机抽样预定长度的子序列来创建训练数据集。更常见的是，我们的数据以序列集合的形式出现。考虑以下例子：(i) 一系列文档，每个文档表示为其自身的词语序列，且每个文档都有自己的长度 \(T_i\)；(ii) 患者住院的序列表示，其中每次住院包含多个事件，序列长度大致取决于住院时长。

以前，在处理单个输入时，我们假设它们是从同一底层分布 \(P(X)\) 中独立抽样的。虽然我们仍然假设整个序列（例如，整个文档或患者轨迹）是独立抽样的，但我们不能假设每个时间步到达的数据彼此独立。例如，文档中后面可能出现的词语很大程度上取决于文档前面出现的词语。患者在住院第10天可能接受的药物很大程度上取决于前九天发生的事情。

这并不奇怪。如果我们不相信序列中的元素是相关的，我们一开始就不会费心将它们建模为序列。考虑一下搜索工具和现代电子邮件客户端中流行的自动填充功能的用处。它们之所以有用，正是因为通常可以预测（不完美，但比随机猜测要好）给定某个初始前缀后，序列可能的延续是什么。对于大多数序列模型，我们不要求序列的独立性，甚至不要求平稳性。我们只要求序列本身是从某个固定的整个序列的底层分布中抽样的。

这种灵活的方法允许出现以下现象：(i) 文档的开头和结尾看起来显著不同；(ii) 在住院期间，患者状态要么向康复发展，要么向死亡发展；(iii) 在与推荐系统持续互动的过程中，顾客的品味以可预测的方式演变。

有时我们希望在给定序列结构化输入的情况下预测一个固定的目标 \(y\)（例如，基于电影评论的情感分类）。其他时候，我们希望在给定固定输入的情况下预测一个序列结构化的目标（\(y_1, \ldots, y_T\)）（例如，图像字幕）。还有一些时候，我们的目标是基于序列结构化的输入来预测序列结构化的目标（例如，机器翻译或视频字幕）。这类序列到序列的任务有两种形式：(i) 对齐的：其中每个时间步的输入与相应的目标对齐（例如，词性标注）；(ii) 未对齐的：其中输入和目标不一定表现出步步对应的关系（例如，机器翻译）。

在我们担心处理任何类型的目标之前，我们可以先解决最直接的问题：无监督密度建模（也称为*序列建模*）。在这里，给定一个序列集合，我们的目标是估计概率质量函数，该函数告诉我们看到任何给定序列的可能性，即 \(p(\mathbf{x}_1, \ldots, \mathbf{x}_T)\)。

pytorchmxnetjaxtensorflow

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

%matplotlib inline
from mxnet import autograd, gluon, init, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l

npx.set_np()

%matplotlib inline
import jax
import numpy as np
from jax import numpy as jnp
from d2l import jax as d2l

No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

%matplotlib inline
import tensorflow as tf
from d2l import tensorflow as d2l

9.1.1. 自回归模型

在介绍专门用于处理序列结构化数据的神经网络之前，让我们先看一些实际的序列数据，并建立一些基本的直觉和统计工具。具体来说，我们将关注富时100指数的股价数据（图 9.1.1）。在每个*时间步* \(t \in \mathbb{Z}^+\)，我们观察到该指数在那个时间的价格 \(x_t\)。

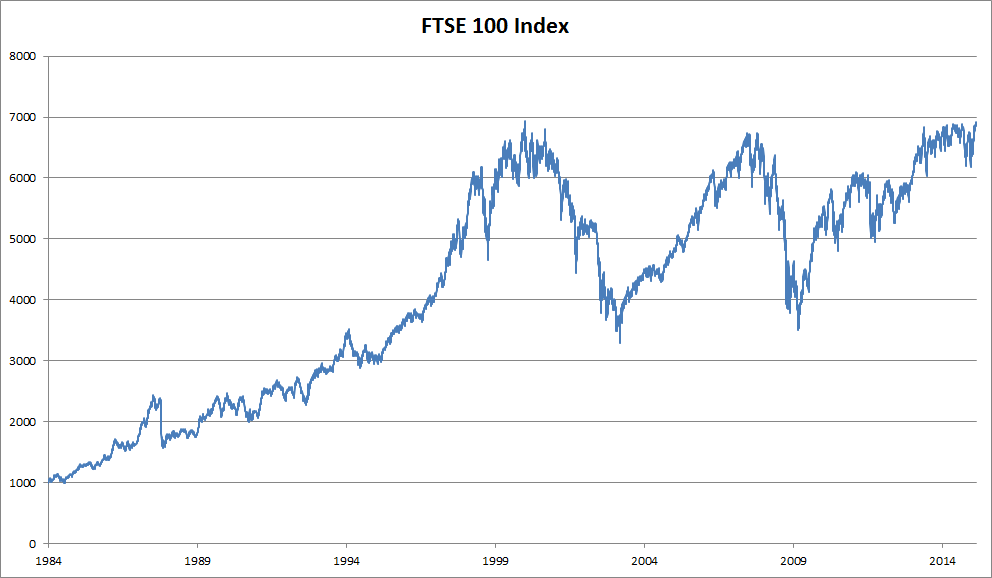
图 9.1.1 约30年间的富时100指数。

现在假设一个交易员想要进行短期交易，根据他们认为指数在下一个时间步会上升还是下降，有策略地进入或退出该指数。在没有任何其他特征（新闻、财务报告数据等）的情况下，预测后续值的唯一可用信号是迄今为止的价格历史。因此，交易员有兴趣知道概率分布

(9.1.1)\[P(x_t \mid x_{t-1}, \ldots, x_1)\]

表示指数在下一个时间步可能取的价格。虽然估计一个连续值随机变量的整个分布可能很困难，但交易员会很乐意专注于该分布的几个关键统计量，特别是期望值和方差。一个估计条件期望的简单策略是

(9.1.2)\[\mathbb{E}[(x_t \mid x_{t-1}, \ldots, x_1)],\]

可以应用线性回归模型（回想一下 3.1节）。这种将信号值回归到该信号先前值上的模型自然地被称为*自回归模型*。这里只有一个主要问题：输入的数量 \(x_{t-1}, \ldots, x_1\) 会根据 \(t\) 的不同而变化。换句话说，输入的数量随着我们遇到的数据量的增加而增加。因此，如果我们想将历史数据作为训练集，我们就会面临每个样本具有不同数量特征的问题。本章接下来的大部分内容将围绕着克服这些挑战的技术，当处理这类*自回归*建模问题时，我们的目标是 \(P(x_t \mid x_{t-1}, \ldots, x_1)\) 或该分布的一些统计量。

一些策略经常出现。首先，我们可能认为，尽管有长序列 \(x_{t-1}, \ldots, x_1\) 可用，但在预测近期未来时可能不需要回溯那么远的历史。在这种情况下，我们可能会满足于以长度为 \(\tau\) 的窗口为条件，只使用 \(x_{t-1}, \ldots, x_{t-\tau}\) 的观测值。直接的好处是，至少对于 \(t > \tau\)，参数的数量总是相同的。这使我们能够训练任何需要固定长度向量作为输入的线性模型或深度网络。其次，我们可以开发出既能维护过去观测值摘要 \(h_t\)（见图 9.1.2）又能同时更新 \(h_t\) 和预测 \(\hat{x}_t\) 的模型。这导致了不仅用 \(\hat{x}_t = P(x_t \mid h_{t})\) 来估计 \(x_t\)，而且还进行 \(h_t = g(h_{t-1}, x_{t-1})\) 形式更新的模型。由于 \(h_t\) 从未被观测到，这些模型也被称为*潜在自回归模型*。

图 9.1.2 一个潜在自回归模型。

为了从历史数据中构建训练数据，通常通过随机抽样窗口来创建样本。总的来说，我们不期望时间会静止。然而，我们通常假设，虽然 \(x_t\) 的具体值可能会改变，但根据先前观测生成每个后续观测的动态不会改变。统计学家称不变的动态为*平稳的*。

9.1.2. 序列模型

有时，尤其是在处理语言时，我们希望估计整个序列的联合概率。这在处理由离散*词元*（如单词）组成的序列时是一项常见的任务。通常，这些估计函数被称为*序列模型*，对于自然语言数据，它们被称为*语言模型*。序列建模领域受自然语言处理的推动如此之大，以至于我们经常将序列模型描述为“语言模型”，即使在处理非语言数据时也是如此。语言模型在各种原因下都很有用。有时我们想评估句子的可能性。例如，我们可能希望比较机器翻译系统或语音识别系统生成的两个候选输出的自然度。但语言建模不仅给了我们*评估*可能性的能力，还给了我们*采样*序列的能力，甚至可以优化以找到最可能的序列。

虽然语言建模乍一看可能不像一个自回归问题，但我们可以通过应用概率的链式法则，将序列 \(p(x_1, \ldots, x_T)\) 的联合密度以从左到右的方式分解为条件密度的乘积，从而将语言建模简化为自回归预测。

(9.1.3)\[P(x_1, \ldots, x_T) = P(x_1) \prod_{t=2}^T P(x_t \mid x_{t-1}, \ldots, x_1).\]

请注意，如果我们处理的是像单词这样的离散信号，那么自回归模型必须是一个概率分类器，输出一个关于词汇表的完整概率分布，用于预测在给定左侧上下文的情况下下一个将出现的单词。

9.1.2.1. 马尔可夫模型

现在假设我们希望采用上面提到的策略，即只以前 \(\tau\) 个时间步为条件，即 \(x_{t-1}, \ldots, x_{t-\tau}\)，而不是整个序列历史 \(x_{t-1}, \ldots, x_1\)。每当我们可以在不损失任何预测能力的情况下舍弃前 \(\tau\) 步之外的历史时，我们就说该序列满足*马尔可夫条件*，即*给定近期历史，未来与过去条件独立*。当 \(\tau = 1\) 时，我们说数据由*一阶马尔可夫模型*表征，当 \(\tau = k\) 时，我们说数据由 \(k^{\textrm{th}}\) 阶马尔可夫模型表征。当一阶马尔可夫条件成立时（\(\tau = 1\)），我们的联合概率分解变为每个词在给定前一个*词*的概率的乘积

(9.1.4)\[P(x_1, \ldots, x_T) = P(x_1) \prod_{t=2}^T P(x_t \mid x_{t-1}).\]

我们常常发现，即使我们知道马尔可夫条件只是*近似*成立，使用假设其成立的模型也很有用。对于真实的文本文档，我们包含越多的左侧上下文，就能获得越多的信息。但这些收益会迅速减少。因此，有时我们会妥协，通过训练其有效性依赖于 \(k^{\textrm{th}}\) 阶马尔可夫条件的模型来避免计算和统计上的困难。即使是当今基于RNN和Transformer的大型语言模型，也很少包含超过数千个单词的上下文。

对于离散数据，一个真正的马尔可夫模型只是简单地计算每个词在每种上下文中出现的次数，从而产生 \(P(x_t \mid x_{t-1})\) 的相对频率估计。当数据只取离散值时（如在语言中），最可能的词序列可以使用动态规划高效地计算出来。

9.1.2.2. 解码顺序

你可能想知道为什么我们把文本序列 \(P(x_1, \ldots, x_T)\) 的因式分解表示为从左到右的条件概率链。为什么不是从右到左，或者其他看起来随机的顺序呢？原则上，以相反的顺序展开 \(P(x_1, \ldots, x_T)\) 并没有什么问题。结果是一个有效的因式分解

(9.1.5)\[P(x_1, \ldots, x_T) = P(x_T) \prod_{t=T-1}^1 P(x_t \mid x_{t+1}, \ldots, x_T).\]

然而，对于语言建模任务，有很多原因偏好以我们阅读的方向（对于大多数语言是从左到右，但对于阿拉伯语和希伯来语是从右到左）对文本进行因式分解。首先，这只是我们思考的一个更自然的方向。毕竟我们每天都阅读文本，这个过程是由我们预测接下来可能出现的单词和短语的能力所引导的。想想你有多少次替别人说完了句子。因此，即使我们没有其他理由偏好这种顺序解码，它们也会很有用，只因为我们对以这种顺序预测时什么应该是可能的有更好的直觉。

其次，通过按顺序进行因式分解，我们可以使用同一个语言模型为任意长的序列分配概率。要将从第 \(1\) 步到第 \(t\) 步的概率转换为扩展到单词 \(t+1\) 的概率，我们只需乘以给定先前词元的附加词元的条件概率：\(P(x_{t+1}, \ldots, x_1) = P(x_{t}, \ldots, x_1) \cdot P(x_{t+1} \mid x_{t}, \ldots, x_1)\)。

第三，我们有更强的预测模型来预测相邻的单词，而不是任意其他位置的单词。虽然所有因式分解的顺序都是有效的，但它们不一定都代表同样简单的预测建模问题。这不仅适用于语言，也适用于其他类型的数据，例如当数据具有因果结构时。例如，我们相信未来的事件不能影响过去。因此，如果我们改变 \(x_t\)，我们可能会影响 \(x_{t+1}\) 之后发生的事情，但反之则不然。也就是说，如果我们改变 \(x_t\)，过去事件的分布不会改变。在某些情况下，这使得预测 \(P(x_{t+1} \mid x_t)\) 比预测 \(P(x_t \mid x_{t+1})\) 更容易。例如，在某些情况下，我们可以找到 \(x_{t+1} = f(x_t) + \epsilon\) 对于一些加性噪声 \(\epsilon\)，而反之则不成立 （Hoyer 等人, 2009）。这是个好消息，因为我们通常感兴趣的是估计正向方向。Peters 等人（2017）的书中对此有更多讨论。我们只是浅尝辄止。

9.1.3. 训练

在我们将注意力集中在文本数据上之前，让我们先用一些连续值的合成数据来试试。

在这里，我们的1000个合成数据将遵循三角函数 sin，应用于时间步的0.01倍。为了让问题更有趣，我们用加性噪声来扰动每个样本。从这个序列中，我们提取训练样本，每个样本都包含特征和标签。

pytorchmxnetjaxtensorflow

class Data(d2l.DataModule):
    def __init__(self, batch_size=16, T=1000, num_train=600, tau=4):
        self.save_hyperparameters()
        self.time = torch.arange(1, T + 1, dtype=torch.float32)
        self.x = torch.sin(0.01 * self.time) + torch.randn(T) * 0.2

data = Data()
d2l.plot(data.time, data.x, 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

class Data(d2l.DataModule):
    def __init__(self, batch_size=16, T=1000, num_train=600, tau=4):
        self.save_hyperparameters()
        self.time = np.arange(1, T + 1, dtype=np.float32)
        self.x = np.sin(0.01 * self.time) + np.random.randn(T) * 0.2

data = Data()
d2l.plot(data.time, data.x, 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

[22:06:39] ../src/storage/storage.cc:196: Using Pooled (Naive) StorageManager for CPU

class Data(d2l.DataModule):
    def __init__(self, batch_size=16, T=1000, num_train=600, tau=4):
        self.save_hyperparameters()
        self.time = jnp.arange(1, T + 1, dtype=jnp.float32)
        key = d2l.get_key()
        self.x = jnp.sin(0.01 * self.time) + jax.random.normal(key,
                                                               [T]) * 0.2

data = Data()
d2l.plot(data.time, data.x, 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

class Data(d2l.DataModule):
    def __init__(self, batch_size=16, T=1000, num_train=600, tau=4):
        self.save_hyperparameters()
        self.time = tf.range(1, T + 1, dtype=tf.float32)
        self.x = tf.sin(0.01 * self.time) + tf.random.normal([T]) * 0.2

data = Data()
d2l.plot(data.time, data.x, 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

首先，我们尝试一个模型，该模型假设数据满足一个 \(\tau^{\textrm{th}}\) 阶马尔可夫条件，因此仅使用过去的 \(\tau\) 个观测值来预测 \(x_t\)。因此，对于每个时间步，我们都有一个标签为 \(y = x_t\) 和特征为 \(\mathbf{x}_t = [x_{t-\tau}, \ldots, x_{t-1}]\) 的样本。敏锐的读者可能已经注意到，这会导致 \(1000-\tau\) 个样本，因为我们缺少 \(y_1, \ldots, y_\tau\) 的足够历史。虽然我们可以用零填充前 \(\tau\) 个序列，但为了简单起见，我们暂时丢弃它们。得到的数据集包含 \(T - \tau\) 个样本，其中模型的每个输入序列长度为 \(\tau\)。我们在前600个样本上创建一个数据迭代器，覆盖了sin函数的一个周期。

pytorchmxnetjaxtensorflow

@d2l.add_to_class(Data)
def get_dataloader(self, train):
    features = [self.x[i : self.T-self.tau+i] for i in range(self.tau)]
    self.features = torch.stack(features, 1)
    self.labels = self.x[self.tau:].reshape((-1, 1))
    i = slice(0, self.num_train) if train else slice(self.num_train, None)
    return self.get_tensorloader([self.features, self.labels], train, i)

@d2l.add_to_class(Data)
def get_dataloader(self, train):
    features = [self.x[i : self.T-self.tau+i] for i in range(self.tau)]
    self.features = np.stack(features, 1)
    self.labels = self.x[self.tau:].reshape((-1, 1))
    i = slice(0, self.num_train) if train else slice(self.num_train, None)
    return self.get_tensorloader([self.features, self.labels], train, i)

@d2l.add_to_class(Data)
def get_dataloader(self, train):
    features = [self.x[i : self.T-self.tau+i] for i in range(self.tau)]
    self.features = jnp.stack(features, 1)
    self.labels = self.x[self.tau:].reshape((-1, 1))
    i = slice(0, self.num_train) if train else slice(self.num_train, None)
    return self.get_tensorloader([self.features, self.labels], train, i)

@d2l.add_to_class(Data)
def get_dataloader(self, train):
    features = [self.x[i : self.T-self.tau+i] for i in range(self.tau)]
    self.features = tf.stack(features, 1)
    self.labels = tf.reshape(self.x[self.tau:], (-1, 1))
    i = slice(0, self.num_train) if train else slice(self.num_train, None)
    return self.get_tensorloader([self.features, self.labels], train, i)

在这个例子中，我们的模型将是一个标准的线性回归。

pytorchmxnetjaxtensorflow

model = d2l.LinearRegression(lr=0.01)
trainer = d2l.Trainer(max_epochs=5)
trainer.fit(model, data)

model = d2l.LinearRegression(lr=0.01)
trainer = d2l.Trainer(max_epochs=5)
trainer.fit(model, data)

model = d2l.LinearRegression(lr=0.01)
trainer = d2l.Trainer(max_epochs=5)
trainer.fit(model, data)

model = d2l.LinearRegression(lr=0.01)
trainer = d2l.Trainer(max_epochs=5)
trainer.fit(model, data)

9.1.4. 预测

为了评估我们的模型，我们首先检查它在单步预测中的表现如何。

pytorchmxnetjaxtensorflow

onestep_preds = model(data.features).detach().numpy()
d2l.plot(data.time[data.tau:], [data.labels, onestep_preds], 'time', 'x',
         legend=['labels', '1-step preds'], figsize=(6, 3))

onestep_preds = model(data.features).asnumpy()
d2l.plot(data.time[data.tau:], [data.labels, onestep_preds], 'time', 'x',
         legend=['labels', '1-step preds'], figsize=(6, 3))

onestep_preds = model.apply({'params': trainer.state.params}, data.features)
d2l.plot(data.time[data.tau:], [data.labels, onestep_preds], 'time', 'x',
         legend=['labels', '1-step preds'], figsize=(6, 3))

onestep_preds = model(data.features).numpy()
d2l.plot(data.time[data.tau:], [data.labels, onestep_preds], 'time', 'x',
         legend=['labels', '1-step preds'], figsize=(6, 3))

这些预测看起来不错，即使在接近结尾的 \(t=1000\) 时也是如此。

但是，如果我们只观察到时间步604（n_train + tau）之前的数据，并希望对未来几步进行预测呢？不幸的是，我们不能直接计算时间步609的单步预测，因为我们不知道相应的输入，我们只看到了 \(x_{604}\)。我们可以通过将我们之前的预测作为模型输入来进行后续预测，一步一步地向前推进，直到达到期望的时间步来解决这个问题。

(9.1.6)\[\begin{split}\begin{aligned} \hat{x}_{605} &= f(x_{601}, x_{602}, x_{603}, x_{604}), \\ \hat{x}_{606} &= f(x_{602}, x_{603}, x_{604}, \hat{x}_{605}), \\ \hat{x}_{607} &= f(x_{603}, x_{604}, \hat{x}_{605}, \hat{x}_{606}),\\ \hat{x}_{608} &= f(x_{604}, \hat{x}_{605}, \hat{x}_{606}, \hat{x}_{607}),\\ \hat{x}_{609} &= f(\hat{x}_{605}, \hat{x}_{606}, \hat{x}_{607}, \hat{x}_{608}),\\ &\vdots\end{aligned}\end{split}\]

通常，对于一个观测到的序列 \(x_1, \ldots, x_t\)，其在时间步 \(t+k\) 的预测输出 \(\hat{x}_{t+k}\) 称为 \(k\)步前预测。由于我们观测到了 \(x_{604}\)，其 \(k\) 步前预测是 \(\hat{x}_{604+k}\)。换句话说，我们将不得不继续使用我们自己的预测来进行多步前预测。让我们看看效果如何。

pytorchmxnetjaxtensorflow

multistep_preds = torch.zeros(data.T)
multistep_preds[:] = data.x
for i in range(data.num_train + data.tau, data.T):
    multistep_preds[i] = model(
        multistep_preds[i - data.tau:i].reshape((1, -1)))
multistep_preds = multistep_preds.detach().numpy()

d2l.plot([data.time[data.tau:], data.time[data.num_train+data.tau:]],
         [onestep_preds, multistep_preds[data.num_train+data.tau:]], 'time',
         'x', legend=['1-step preds', 'multistep preds'], figsize=(6, 3))

multistep_preds = np.zeros(data.T)
multistep_preds[:] = data.x
for i in range(data.num_train + data.tau, data.T):
    multistep_preds[i] = model(
        multistep_preds[i - data.tau:i].reshape((1, -1)))
multistep_preds = multistep_preds.asnumpy()

d2l.plot([data.time[data.tau:], data.time[data.num_train+data.tau:]],
         [onestep_preds, multistep_preds[data.num_train+data.tau:]], 'time',
         'x', legend=['1-step preds', 'multistep preds'], figsize=(6, 3))

multistep_preds = jnp.zeros(data.T)
multistep_preds = multistep_preds.at[:].set(data.x)
for i in range(data.num_train + data.tau, data.T):
    pred = model.apply({'params': trainer.state.params},
                       multistep_preds[i - data.tau:i].reshape((1, -1)))
    multistep_preds = multistep_preds.at[i].set(pred.item())

d2l.plot([data.time[data.tau:], data.time[data.num_train+data.tau:]],
         [onestep_preds, multistep_preds[data.num_train+data.tau:]], 'time',
         'x', legend=['1-step preds', 'multistep preds'], figsize=(6, 3))

multistep_preds = tf.Variable(tf.zeros(data.T))
multistep_preds[:].assign(data.x)
for i in range(data.num_train + data.tau, data.T):
    multistep_preds[i].assign(tf.reshape(model(
        tf.reshape(multistep_preds[i-data.tau : i], (1, -1))), ()))

d2l.plot([data.time[data.tau:], data.time[data.num_train+data.tau:]],
         [onestep_preds, multistep_preds[data.num_train+data.tau:]], 'time',
         'x', legend=['1-step preds', 'multistep preds'], figsize=(6, 3))

不幸的是，在这种情况下我们惨败了。预测在几步之后很快就衰减为一个常数。为什么算法在预测更远的未来时表现得这么差？最终，这是因为误差会累积。假设在第1步之后我们有一些误差 \(\epsilon_1 = \bar\epsilon\)。现在第2步的*输入*被 \(\epsilon_1\) 扰动，因此我们遭受了一些量级为 \(\epsilon_2 = \bar\epsilon + c \epsilon_1\) 的误差，对于某个常数 \(c\)，依此类推。预测会迅速偏离真实的观测值。你可能已经熟悉这种常见现象。例如，未来24小时的天气预报往往相当准确，但超过这个时间，准确性会迅速下降。我们将在本章及以后讨论改进这种情况的方法。

让我们通过计算整个序列在 \(k = 1, 4, 16, 64\) 时的预测，来更仔细地看看 \(k\) 步前预测的困难。

pytorchmxnetjaxtensorflow

def k_step_pred(k):
    features = []
    for i in range(data.tau):
        features.append(data.x[i : i+data.T-data.tau-k+1])
    # The (i+tau)-th element stores the (i+1)-step-ahead predictions
    for i in range(k):
        preds = model(torch.stack(features[i : i+data.tau], 1))
        features.append(preds.reshape(-1))
    return features[data.tau:]

steps = (1, 4, 16, 64)
preds = k_step_pred(steps[-1])
d2l.plot(data.time[data.tau+steps[-1]-1:],
         [preds[k - 1].detach().numpy() for k in steps], 'time', 'x',
         legend=[f'{k}-step preds' for k in steps], figsize=(6, 3))

def k_step_pred(k):
    features = []
    for i in range(data.tau):
        features.append(data.x[i : i+data.T-data.tau-k+1])
    # The (i+tau)-th element stores the (i+1)-step-ahead predictions
    for i in range(k):
        preds = model(np.stack(features[i : i+data.tau], 1))
        features.append(preds.reshape(-1))
    return features[data.tau:]

steps = (1, 4, 16, 64)
preds = k_step_pred(steps[-1])
d2l.plot(data.time[data.tau+steps[-1]-1:],
         [preds[k - 1].asnumpy() for k in steps], 'time', 'x',
         legend=[f'{k}-step preds' for k in steps], figsize=(6, 3))

def k_step_pred(k):
    features = []
    for i in range(data.tau):
        features.append(data.x[i : i+data.T-data.tau-k+1])
    # The (i+tau)-th element stores the (i+1)-step-ahead predictions
    for i in range(k):
        preds = model.apply({'params': trainer.state.params},
                            jnp.stack(features[i : i+data.tau], 1))
        features.append(preds.reshape(-1))
    return features[data.tau:]

steps = (1, 4, 16, 64)
preds = k_step_pred(steps[-1])
d2l.plot(data.time[data.tau+steps[-1]-1:],
         [np.asarray(preds[k-1]) for k in steps], 'time', 'x',
         legend=[f'{k}-step preds' for k in steps], figsize=(6, 3))

def k_step_pred(k):
    features = []
    for i in range(data.tau):
        features.append(data.x[i : i+data.T-data.tau-k+1])
    # The (i+tau)-th element stores the (i+1)-step-ahead predictions
    for i in range(k):
        preds = model(tf.stack(features[i : i+data.tau], 1))
        features.append(tf.reshape(preds, -1))
    return features[data.tau:]

steps = (1, 4, 16, 64)
preds = k_step_pred(steps[-1])
d2l.plot(data.time[data.tau+steps[-1]-1:],
         [preds[k - 1].numpy() for k in steps], 'time', 'x',
         legend=[f'{k}-step preds' for k in steps], figsize=(6, 3))

这清楚地说明了当我们试图预测更远的未来时，预测质量是如何变化的。虽然4步前的预测看起来还不错，但超过这个范围的几乎都没用了。

9.1.5. 小结

内插和外推的难度有很大的区别。因此，如果你有一个序列，在训练时一定要尊重数据的时间顺序，即永远不要在未来的数据上进行训练。对于这类数据，序列模型需要专门的统计工具进行估计。两种流行的选择是自回归模型和潜在变量自回归模型。对于因果模型（例如，时间向前），估计正向通常比反向容易得多。对于观测到时间步 \(t\) 的序列，其在时间步 \(t+k\) 的预测输出是 \(k\)步前预测。随着我们通过增加 \(k\) 来预测更远的时间，误差会累积，预测的质量会下降，通常是急剧下降。

9.1.6. 练习

1. 改进本节实验中的模型。

   1. 是否可以纳入超过过去四个的观测值？你到底需要多少个？

   2. 如果没有噪声，你需要多少个过去的观测值？提示：你可以将 \(\sin\) 和 \(\cos\) 写成一个微分方程。

   3. 你能在保持特征总数不变的情况下，纳入更早的观测值吗？这能提高准确性吗？为什么？

   4. 改变神经网络架构并评估性能。你可以用更多的轮次来训练新模型。你观察到了什么？

2. 一位投资者想找到一只好的证券来购买。他们查看过去的回报来决定哪一只可能会表现得好。这种策略可能会出什么问题？

3. 因果关系也适用于文本吗？在多大程度上适用？

4. 举一个例子，说明什么时候可能需要潜在自回归模型来捕捉数据的动态。

pytorchmxnetjaxtensorflow

讨论

讨论

讨论

讨论