17.1. 马尔可夫决策过程 (MDP)
在 Colab 中打开 Notebook
在 Colab 中打开 Notebook
在 Colab 中打开 Notebook
在 Colab 中打开 Notebook
在 SageMaker Studio Lab 中打开 Notebook

在本节中，我们将讨论如何使用马尔可夫决策过程 (MDP) 来构建强化学习问题，并详细描述 MDP 的各个组成部分。

17.1.1. MDP的定义

马尔可夫决策过程 (MDP) (Bellman, 1957) 是一个模型，用于描述当不同动作应用于系统时，系统状态如何演变。一个 MDP 由几个不同的量共同构成。

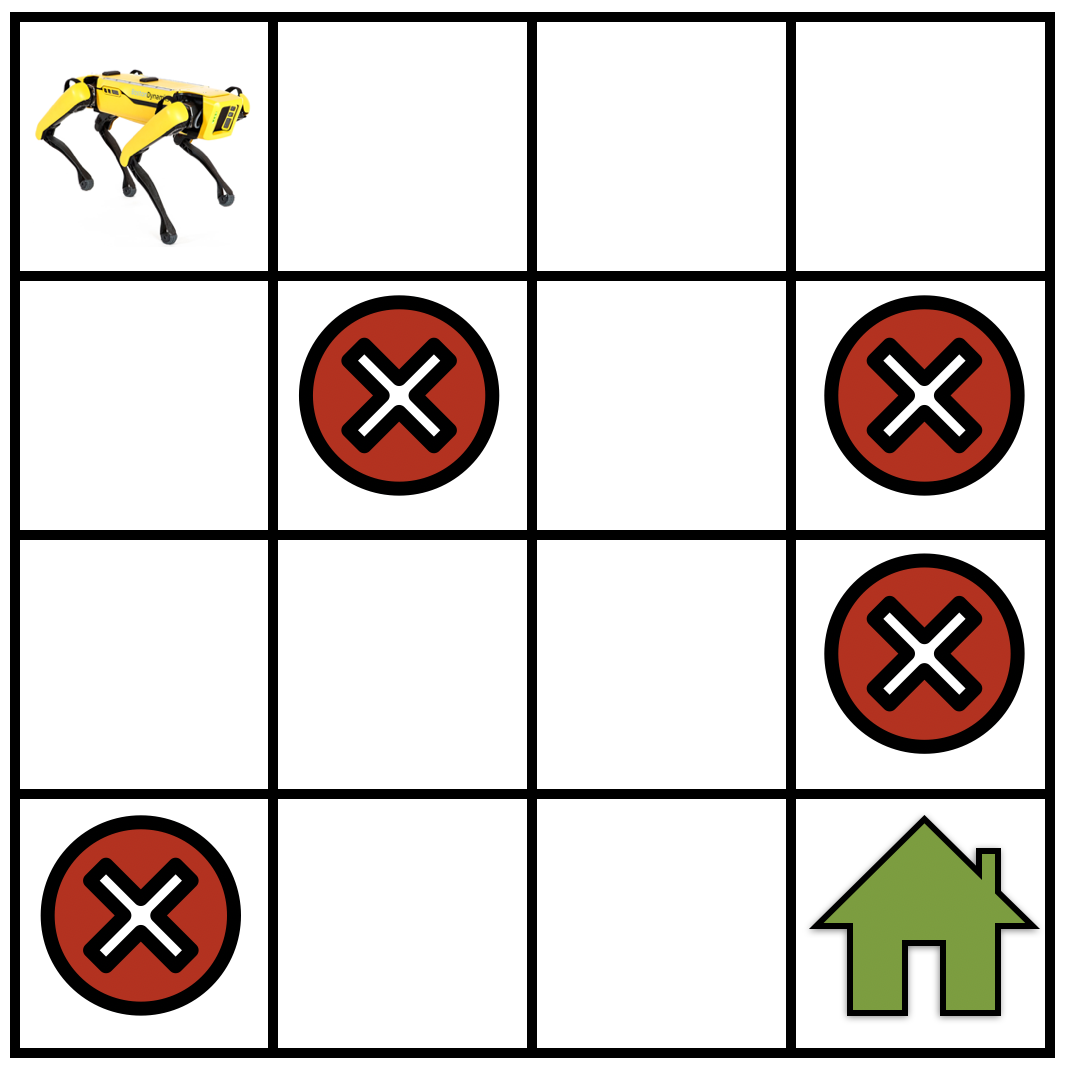
../_images/mdp.png

图 17.1.1 一个简单的网格世界导航任务，机器人不仅要找到通往目标位置（绿色房子）的路径，还要避开陷阱位置（红色叉号）。

  • 设 \(\mathcal{S}\) 为 MDP 中的状态集合。举一个具体的例子，参见 图 17.1.1，一个在网格世界中导航的机器人。在这种情况下，\(\mathcal{S}\) 对应于机器人在任何给定时间步可以处于的位置集合。

  • 设 \(\mathcal{A}\) 为机器人在每个状态可以采取的动作集合，例如“前进”、“右转”、“左转”、“停在原地”等。动作可以将机器人的当前状态改变为集合 \(\mathcal{S}\) 内的某个其他状态。

  • 我们可能无法 *确切* 知道机器人的移动方式，而只能知道一个近似值。我们在强化学习中对这种情况进行建模如下：如果机器人采取“前进”动作，它可能有很小的概率停在当前状态，有另一个很小的概率“向左转”等。从数学上讲，这相当于定义一个“转移函数” \(T: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \to [0,1]\)，使得 \(T(s, a, s') = P(s' \mid s, a)\)，使用条件概率来表示在状态 \(s\) 下采取动作 \(a\) 后到达状态 \(s'\) 的概率。转移函数是一个概率分布，因此我们有 \(\sum_{s' \in \mathcal{S}} T(s, a, s') = 1\) 对所有 \(s \in \mathcal{S}\) 和 \(a \in \mathcal{A}\) 成立，即机器人采取动作后必须进入某个状态。

  • 我们现在使用“奖励” \(r: \mathcal{S} \times \mathcal{A} \to \mathbb{R}\) 的概念来构建哪些动作有用、哪些动作无用的概念。我们说，如果机器人在状态 \(s\) 下采取动作 \(a\)，它会得到一个奖励 \(r(s,a)\)。如果奖励 \(r(s, a)\) 很大，这表明在状态 \(s\) 下采取动作 \(a\) 对于实现机器人的目标（即到达绿色房子）更有用。如果奖励 \(r(s, a)\) 很小，那么动作 \(a\) 对于实现这个目标就没那么有用。需要注意的是，奖励是由用户（创建强化学习算法的人）根据目标设计的。

17.1.2. 回报和折扣因子

上述不同组件共同构成一个马尔可夫决策过程 (MDP)

(17.1.1)\[\textrm{MDP}: (\mathcal{S}, \mathcal{A}, T, r).\]

现在让我们考虑机器人从一个特定状态 \(s_0 \in \mathcal{S}\) 开始，并持续采取动作，从而产生一条轨迹

(17.1.2)\[\tau = (s_0, a_0, r_0, s_1, a_1, r_1, s_2, a_2, r_2, \ldots).\]

在每个时间步 \(t\)，机器人处于状态 \(s_t\) 并采取动作 \(a_t\)，从而产生奖励 \(r_t = r(s_t, a_t)\)。一条轨迹的*回报*是机器人沿该轨迹获得的总奖励

(17.1.3)\[R(\tau) = r_0 + r_1 + r_2 + \cdots.\]

强化学习的目标是找到一条具有最大*回报*的轨迹。

想象一下这种情况，机器人在网格世界中持续移动却永远无法到达目标位置。在这种情况下，轨迹中的状态和动作序列可能是无限长的，任何这样无限长轨迹的*回报*都将是无限的。为了使强化学习的表述在这种轨迹下仍然有意义，我们引入了折扣因子 \(\gamma < 1\) 的概念。我们将折扣*回报*写为

(17.1.4)\[R(\tau) = r_0 + \gamma r_1 + \gamma^2 r_2 + \cdots = \sum_{t=0}^\infty \gamma^t r_t.\]

请注意，如果 \(\gamma\) 非常小，机器人在遥远的未来（比如 \(t = 1000\)）获得的奖励会因为因子 \(\gamma^{1000}\) 而被大幅折扣。这鼓励机器人选择能实现其目标的短轨迹，即在网格世界示例中到达绿色房子（见 图 17.1.1）。对于较大的折扣因子值，比如 \(\gamma = 0.99\)，机器人被鼓励去*探索*，然后找到到达目标位置的最佳轨迹。

17.1.3. 关于马尔可夫假设的讨论

让我们考虑一个新的机器人，其中状态 \(s_t\) 仍然是位置，但动作 \(a_t\) 是机器人对其轮子施加的加速度，而不是像“前进”这样的抽象命令。如果这个机器人在状态 \(s_t\) 时具有非零速度，那么下一个位置 \(s_{t+1}\) 不仅是过去位置 \(s_t\) 和加速度 \(a_t\) 的函数，还与机器人在时间 \(t\) 的速度有关，而速度与 \(s_t - s_{t-1}\) 成正比。这表明我们应该有

(17.1.5)\[s_{t+1} = \textrm{某个函数}(s_t, a_t, s_{t-1});\]

在我们这个例子中，“某个函数”将是牛顿运动定律。这与我们仅仅依赖于 \(s_t\) 和 \(a_t\) 的转移函数有很大不同。

马尔可夫系统是指所有下一个状态 \(s_{t+1}\) 仅是当前状态 \(s_t\) 和在当前状态下采取的动作 \(a_t\) 的函数的系统。在马尔可夫系统中，下一个状态不依赖于过去采取的动作或机器人过去所处的状态。例如，上面提到的以加速度为动作的新机器人就不是马尔可夫的，因为下一个位置 \(s_{t+1}\) 通过速度依赖于前一个状态 \(s_{t-1}\)。系统的马尔可夫性质似乎是一个限制性假设，但事实并非如此。马尔可夫决策过程仍然能够模拟非常广泛的真实系统。例如，对于我们的新机器人，如果我们将状态 \(s_t\) 选择为元组 \((\textrm{位置}, \textrm{速度})\)，那么该系统就是马尔可夫的，因为它的下一个状态 \((\textrm{位置}_{t+1}, \textrm{速度}_{t+1})\) 仅取决于当前状态 \((\textrm{位置}_t, \textrm{速度}_t)\) 和当前状态的动作 \(a_t\)。

17.1.4. 小结

强化学习问题通常使用马尔可夫决策过程来建模。马尔可夫决策过程 (MDP) 由一个四元组 \((\mathcal{S}, \mathcal{A}, T, r)\) 定义，其中 \(\mathcal{S}\) 是状态空间，\(\mathcal{A}\) 是动作空间，\(T\) 是编码 MDP 转移概率的转移函数，\(r\) 是在特定状态下采取动作获得的即时奖励。

17.1.5. 练习

  1. 假设我们想设计一个 MDP 来模拟 MountainCar 问题。

    1. 状态集会是什么？

    2. 动作集会是什么？

    3. 可能的奖励函数会是什么？

  2. 你将如何为一个像 Pong 游戏 这样的 Atari 游戏设计 MDP？

讨论